In the real estate market, maintaining accurate and current property valuations is essential. Property values can be influenced by a variety of local factors, such as the introduction of new amenities, changes in crime rates, and other shifts in the neighborhood. By continuously adjusting property valuations to reflect these local changes, we ensure that buyers and sellers have the most accurate pricing information
Design Technique : Range Query
To adjust property valuations based on local market conditions efficiently, we can use the Segment Tree with Lazy Propagation algorithm. This data structure is well-suited for handling range queries and updates, making it ideal for our use case where frequent adjustments to property valuations are necessary.
Segment Tree
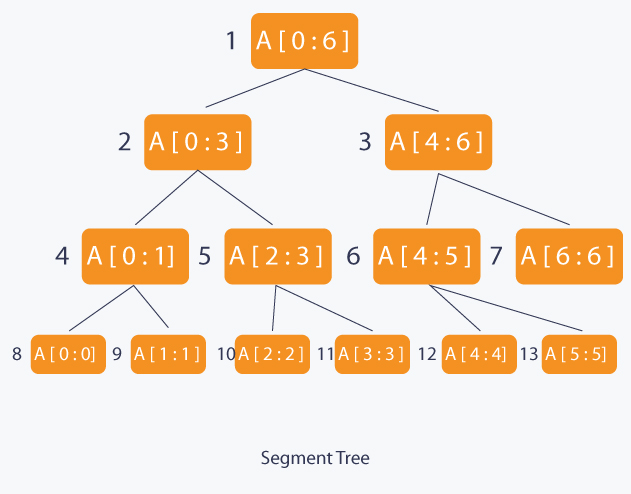
Segment tree or segtree is a basically a binary tree used for storing the intervals or segments. Each node in the segment tree represents an interval. Consider an array A of size N and a corresponding segtree T:
- The root of T will represent the whole array A[0:N-1].
- Each leaf in the segtree T will represent a single element A[i] such that 0 <= i < N.
- The internal nodes in the segtree tree T represent union of elementary intervals A[i:j] where 0 <= i < j < N.
Lazy Propogation
This technique is used to defer updates to segments until necessary, which optimizes the update operations. When an update is required for a segment, we mark it as “lazy,” indicating that this segment needs to be updated. This allows us to batch update operations and apply them only when necessary, improving performance.
Implementation
- Initialize the Segment Tree : Create a class for the segment tree and define two arrays: one for the segment tree and one for lazy propagation.
- Build the Segment Tree :build the segment tree from a given array and recursively split the array into two halves until you reach individual elements.Store the sum of elements at each node.
- Handle Lazy Propagation : Write a function to apply pending updates stored in the lazy array to the current node.
- Update a Range : Write a function to update a range of elements.
- Write a function to query the sum of a range of elements.
Time and Space Complexity
- Time Complexity:
O(logN)for minimum range query. - Space Complexity:
O(N)

 Zestimate- A Property Valuation Tool
Zestimate- A Property Valuation Tool